Zeitdiskretisierungen hoher Ordnung für Strömungen mit freier Oberfläche (2010-2016)

DFG Schwerpunktprogramm 1506: Transport Processes at Fluidic Interfaces

Teilnehmer (AM3)

• Eberhard Bänsch
• Stephan Weller
• Martin Weismann

Ziele

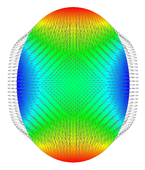Oszillierender Tropfen: Ein einfaches Beispiel kapillarer Strömung, an dem verschiedene Zeitdiskretisierungsmethoden studiert werden.

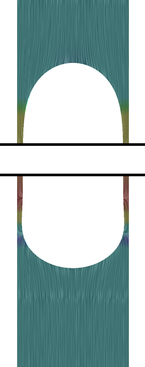Taylorblase: Eine aufsteigende Blase in einem Behälter, an der experimentelle Messungen mit Simulationsergebnissen verglichen werden.

Die fundamentalen Probleme in der numerischen Approximation von Mehrphasen-Systemen, oder allgemeiner der Behandlung von Strömungen mit kapillaren freien Rändern, sind die Darstellung der freien Oberfläche, die Auswertung der Krümmung, die Behandlung der Unstetigkeiten (am wichtigsten ist dabei der Sprung im Druck) und die Zeitdiskretisierungsstrategie um die Strömungsberechnung von der Geometrieberechnung zu entkoppeln.

Während für die ersten drei Probleme eine große Zahl von Techniken in der Literatur der letzten beiden Jahrzehnte zu finden sind, ist das letzte Problem der effizienten Zeitdiskretisierung weitgehend ignoriert worden. Die Mehrzahl der existierenden Zugänge entkoppeln einfach die Strömung von der Geometrie durch einen einfache Trennung: Man verwendet einfach die Geometriedaten des vorhergehenden Zeitschritts in der Strömungsberechnung. Diese Strategie führt aber zu a) einer ernsten kapillaren CFL-Bedingung und b) konvergiert höchstens mit erster Ordnung in der Zeit. Es gibt semi-implizite Zeitdiskretisierungen, die Problem a) vermeiden, diese sind aber immer noch nur von erster Ordnung und zudem in manchen Situationen sehr dissipativ.

Um die Simulationsergebnisse zu validieren, wurden sowohl Messungen experimenteller Gruppen als auch Simulationen anderer numerischer Gruppen verwendet.

Im Laufe dieses Projekts wurden verschiedene teilweise implizite Zeitdiskretisierungen implementiert, die bedingungslos stabil und nur mimimal dissipativ sind. Diese Methoden wurden auch auf flexible Änderungen der Geometrie übertragen.